福岡県公立高校入試数学の平面図形代表問題解説です。
平面図形(円と正三角形)
半径が4cmである円Oがある。AB=AC,∠EAC=∠DAB,∠BAC=60°,点Cを含まない弧ADと弧BDの長さの比が3:1のとき、△ADCの面積を求めよ。
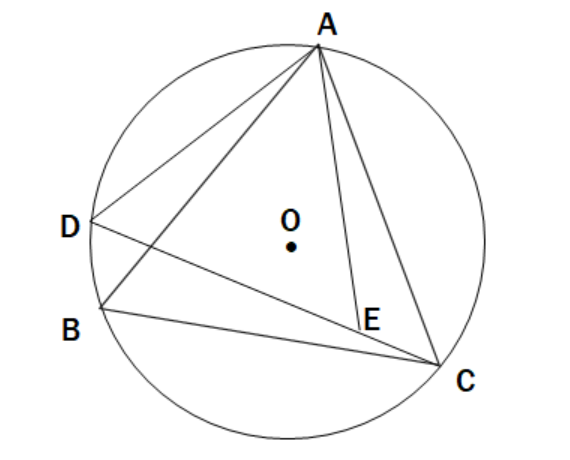
問題を解く上でのポイント
- △ABCは、仮定(問題)より頂角が60°の二等三角形になるので、正三角形である。
- 円に内接する正三角形の中心は、「重心」でもある。
- △AODは、仮定(問題)より弧AD:弧BD=3:1より∠AOD=90°となり、直角二等辺三角形である。
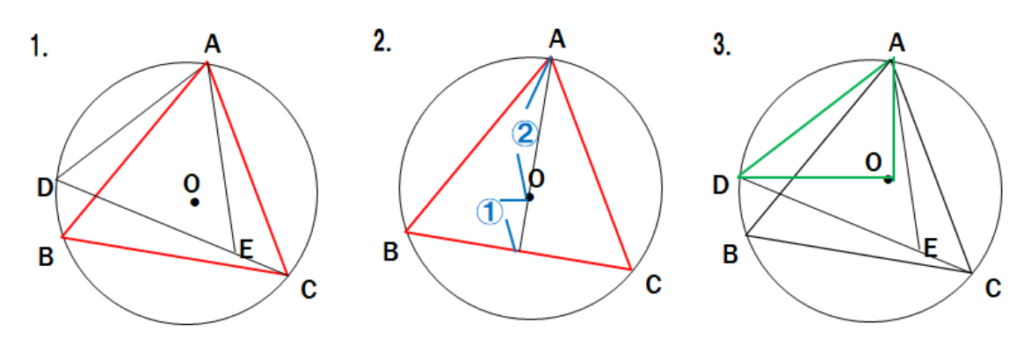
普段の勉強から「キーワード」が出たら、その「キーワード」について全部まとめておくといいでしょう。たとえば今回であれば、「二等辺三角形」円に内接する」「正三角形」「直角三角形」についてどれだけの性質や公式が言えるでしょうか。
内接するであれば、「円に内接する四角形の定理」「円に内接する正三角形の性質」「外接円の性質・公式」「内接円の性質・公式」ぐらいまではパッと出てくるようになっておかないと、修猷館、城南高校を目指す人にとっては厳しいです。
解説
ポイントに留意して、求める三角形の各辺の長さを求めて、面積を出す。

解答
三角形の面積を求める公式(底辺×高さ÷2)より
=DC×AH÷2
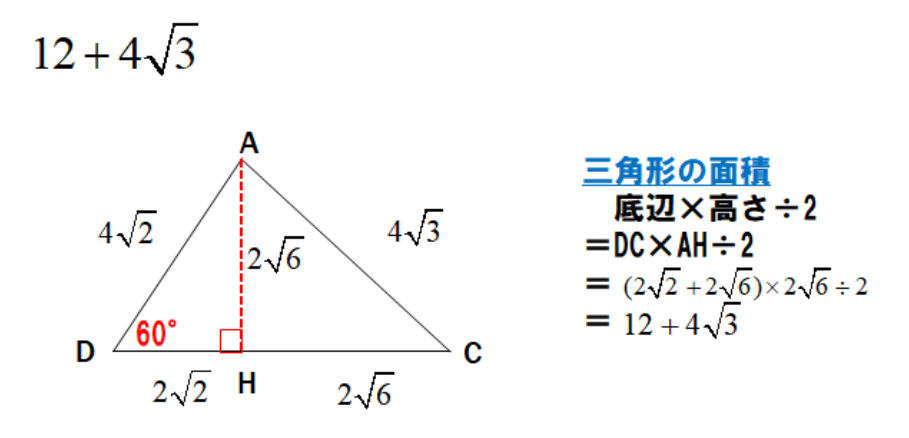


コメント